球形麦克风阵列设计

音频信号处理中，麦克风是最基本的信号接收设备之一。将麦克风组成阵列的主要目的是通过多个麦克风的信息，可以解决很多实际问题：回声、噪声的抑制；视频会议；虚拟现实技术；场景分析等。在声源定位中，阵列几何必须是事先已知的，而且某些规则几何形状的应用可以有效地减少运算量。因此，针对麦克风的设计，提出了一种等距离分布方法，即球面上任意麦克风与相邻麦克风的距离均相等。—— 《基于球傅里叶变换的声源三维空间定位》

问题背景

要设计球形麦克风阵列（SMA），并保证麦克风在球面等距离分布（可以理解为，球面上任一麦克风与相邻麦克风的距离相等），需要给出每个麦克风的具体坐标位置。

麦克风坐标计算

球面上的麦克风最终组成一个规则的凸包多面体（参见Platonic solid），麦克风坐标数值解法其实是一个Thomson problem。

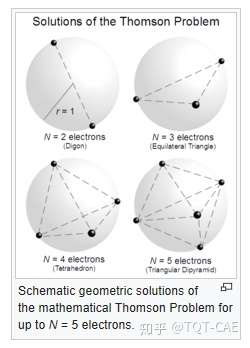
此类问题有多种求解思路（可参考cofludy的博客），其中一种是基于力学原理。大致思路如下：

1)首先建立单位球体，然后将待分布的N个麦克风作为带电粒子，随机分布在该单位球体的表面；

2) 计算每个带电粒子在各个方向上受到的合力大小，然后计算出合力在对应带电粒子上的切线分量；

3) 根据切线分量计算对应带电粒子沿切向运动飞出该单位球体表面的坐标，然后对每一带电粒子的坐标沿径向进行归一化，使所有带电粒子再次回到该单位球体的表面；

4) 步骤2)、3)循环若干次，当各带电粒子所受合力均小于一设定值时，得到各带电粒子的球面均勾分布，即为N个麦克风在该球形的阵列分布。

详细的算法步骤可参考专利描述：一种3D录音系统球面麦克风阵列分布方法【北京大学】

幸运的是，网上有一段现成的MATLAB代码，可通过链接查看，源代码如下：

function []=main()
N=12; %点数量
a=rand(N,1)*2*pi;%根据随机求面均匀分布，先生成一个初始状态
b=asin(rand(N,1)*2-1);
r0=[cos(a).*cos(b),sin(a).*cos(b),sin(b)];
v0=zeros(size(r0));
G=1e-2;%斥力常数，试验这个值比较不错
for ii=1:200%模拟200步，一般已经收敛，其实可以在之下退出
    [rn,vn]=countnext(r0,v0,G);%更新状态
    r0=rn;v0=vn;
end
plot3(rn(:,1),rn(:,2),rn(:,3),'.');hold on;%画结果
[xx,yy,zz]=sphere(50);
h2=surf(xx,yy,zz); %画一个单位球做参考
set(h2,'edgecolor','none','facecolor','r','facealpha',0.7);
axis equal;
axis([-1 1 -1 1 -1 1]);
hold off;
end

function [rn vn]=countnext(r,v,G) %更新状态的函数
%r存放每点的x，y，z数据，v存放每点的速度数据
num=size(r,1);
dd=zeros(3,num,num); %各点间的矢量差
for m=1:num-1
    for n=m+1:num
        dd(:,m,n)=(r(m,:)-r(n,:))';
        dd(:,n,m)=-dd(:,m,n);
    end
end
L=sqrt(sum(dd.^2,1));%各点间的距离
L(L<1e-2)=1e-2; %距离过小限定
F=sum(dd./repmat(L.^3,[3 1 1]),3)';%计算合力

Fr=r.*repmat(dot(F,r,2),[1 3]); %计算合力径向分量
Fv=F-Fr; %切向分量

rn=r+v;  %更新坐标
rn=rn./repmat(sqrt(sum(rn.^2,2)),[1 3]);
vn=v+G*Fv;%跟新速度
end

一开始因为计算机没有安装MATLAB只有Python，代码看着也不多，也有那么一点点Python使用经验，想着用Python重写一遍好了。

结果，困难程度远远超出预期（请原谅我这只菜鸟~）。一边查MATLAB中函数的用法，一边查Numpy中函数的用法，折腾几天还是没能完成。不得已，安装MATLAB后，一步一步确认Python代码的输出结果，又折腾几天最终完成。

Numpy虽然说很多函数和MATLAB非常相似，但有几个地方需要注意：

MATLAB下标索引从1开始，Numpy下标索引从0开始；
MATLAB中多维数组下标依次表示维度 行：列：页，而Numpy中多维数组下标依次表示维度 页：行：列；

计算得到球面麦克风点的坐标后，可利用Scipy.spatial中的ConvexHull函数绘制3D凸包，参考以下链接，源代码如下

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from scipy.spatial import ConvexHull

# 8 points defining the cube corners
pts = np.array([[0, 0, 0], [1, 0, 0], [1, 1, 0], [0, 1, 0],
                [0, 0, 1], [1, 0, 1], [1, 1, 1], [0, 1, 1], ])

hull = ConvexHull(pts)

fig = plt.figure()
ax = fig.add_subplot(111, projection="3d")

# Plot defining corner points
ax.plot(pts.T[0], pts.T[1], pts.T[2], "ko")

# 12 = 2 * 6 faces are the simplices (2 simplices per square face)
for s in hull.simplices:
    s = np.append(s, s[0])  # Here we cycle back to the first coordinate
    ax.plot(pts[s, 0], pts[s, 1], pts[s, 2], "r-")

# Make axis label
for i in ["x", "y", "z"]:
    eval("ax.set_{:s}label('{:s}')".format(i, i))

plt.show()